Định lý Pytago là gì? Công thức tính và áp dụng chuẩn xác

Định lý Pytago là một trong những định lý quan trọng trong toán học. Nhiều người muốn tìm hiểu về nguồn gốc ra đời định lý. Lý thuyết của định lý bao gồm những gì, cách áp dụng được hiệu quả cần lưu ý những vấn đề nào? Toàn bộ các thắc mắc này cần được giải đáp chi tiết qua bài viết ở dưới. 

Định lý Pytago là gì? Nguồn gốc của định lý  

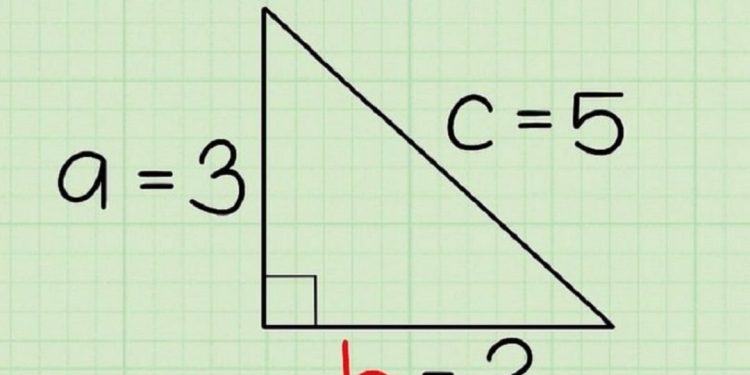
Định lý Pytago là một liên hệ cơ bản trong hình học Euclid với 3 cạnh của 1 tam giác vuông. Ý nghĩa bình phương của cạnh huyền bằng tổng bình phương 2 cạnh còn lại. Công thức cụ thể: (c^2=a^2+b^2), với C: độ dài cạnh huyền, A, B: độ dài 2 cạnh góc vuông.

Trước kia hệ thống chữ số qua nhiều giai đoạn sẽ có sự phát hiện khác nhau và qua ảnh hưởng của các nền văn hóa sẽ thay đổi ít nhiều. Nhân số học từ đó cũng hình thành các hệ thống được tìm hiểu riêng như Nhân số học Pitagorean, Chaldean, Abjad, …

Về nhân số học Pytota thì được các nhà toán học đánh giá là nội dung hoàn chỉnh, chuẩn xác cao so với những hệ thống còn lại. Các con số dùng để thực hiện các phép đo lường hoặc xác định ra số lượng. Nhiều người cho rằng số học không có gì quá to tát và có nhiều ý nghĩa. Tuy nhiên với nhà toán học Pytago thì lại khác, ông luôn miệt mài nghiên cứu để chỉ ra được các con số sẽ là thành tựu to lớn mang lại nhiều đột phá trong bước tiến của nhân loại. 

Con số chính là nền tảng của mọi thứ và được thể hiện quan điểm trong 2 tác phẩm nổi tiếng của ông, đó là Science of Numbers và Theory of Magnitude. Theo nội dung này thì các con số chính là thước đo của năng lượng được truyền tải. Đánh số từ 1-9 thì con số biểu hiện cho 9 tầng năng lượng khác nhau trong mỗi người. 

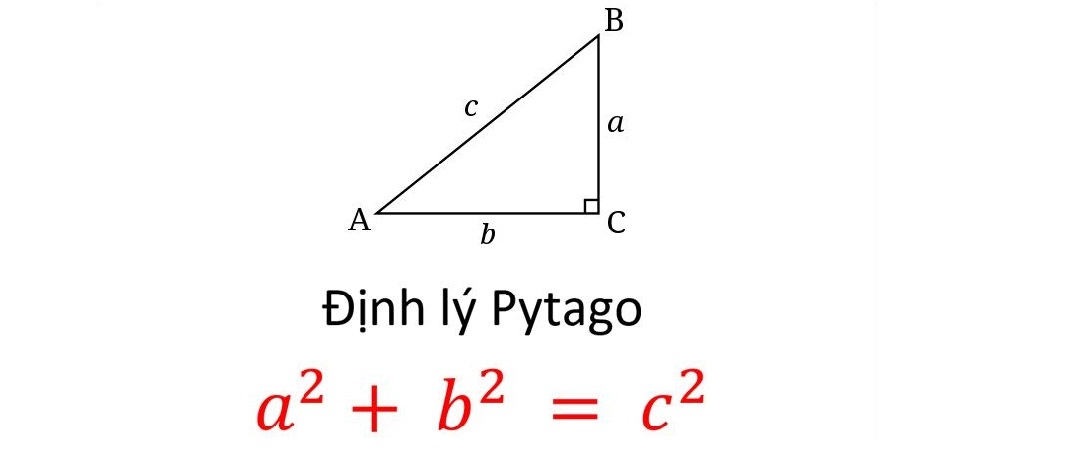
Lý thuyết định lý Pytago 

Lý thuyết về định lý Pytago là điều mà nhiều người muốn tìm hiểu rõ để có căn cứ hiểu hơn về định luật và ứng dụng cho hiệu quả. Hiện nay định luật này sử dụng phổ biến và cực kỳ hữu ích. 

Chứng minh cho định lý Pytago

Nhà toán học Pytago qua các nghiên cứu, tài liệu chứng minh đã hiểu bản chất của định luật. Ngoài ra các nghiên cứu của nhà toán học từ Ấn Độ, Lưỡng Hà, Trung Quốc cũng thực sự góp phần khám phá ra định lý và giúp các chứng minh được chắc chắn, dễ hiểu hơn. 

Chứng minh cho định lý này được cung cấp qua rất nhiều cách thức khác nhau. Có nhiều cách chứng minh để mọi người tìm hiểu như chứng minh bằng hình học, đại số. Định lý cũng được giải nghĩa với nhiều cách khác nhau với không gian đa chiều, không gian phi Euclide,…

Với nội dung hấp dẫn nên định kỳ Pytago đã nhận được về rất nhiều sự quan tâm, góp ý để hoàn thiện. Không chỉ trong lĩnh vực toán học mà các lĩnh vực khác như âm nhạc, văn học, tâm linh…hoàn toàn sử dụng được định luật này. 

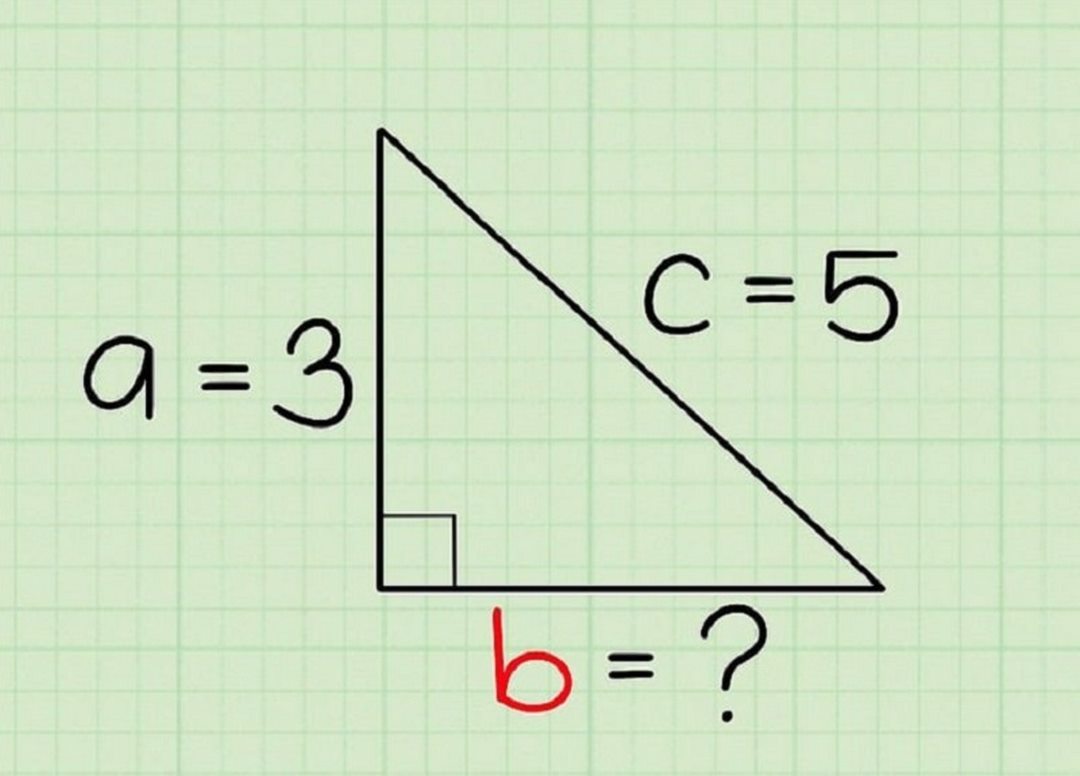
Định lý Pitago chi tiết

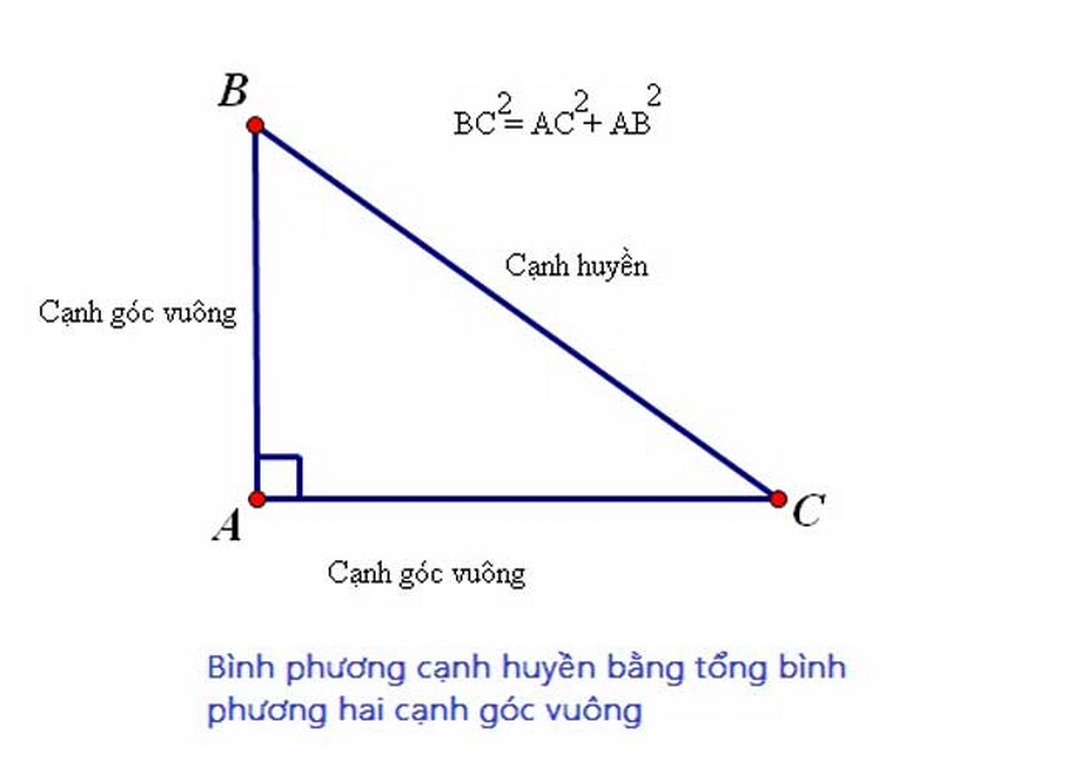
Theo nội dung của định lý thì trong 1 tam giác vuông với 3 cạnh thì công thức sẽ tính bình phương cạnh huyền sẽ bằng tổng bình phương 2 cạnh còn lại. Công thức có dạng: 

(c ^ {2} = a ^ {2} + b ^ {2} )

Còn với Delta ABC có vuông tại A thì áp dụng công thức: 

(BC ^ {2} = AC ^ {2}  + AB ^ {2})

Khi học định lý Pytago cần lưu ý những gì?

Định lý Pytago hiện nay đã được vào trong chương trình toán học về nghiên cứu và ứng dụng. Và khi học về định lý này muốn hiểu rõ bản chất, ứng dụng làm sao cho hiệu quả, giải bài tập chuẩn xác. Các bạn nên có lưu ý một số vấn đề như sau:

• Tam giác vuông với cạnh huyền luôn cắt ngang qua góc vuông nhưng không đi qua chính góc vuông. Cạnh huyền được biết là một cạnh dài nhất có ở tam giác vuông. 
• C là cạnh huyền trong định lý Pytago, A và B là 2 cạnh của góc vuông
• Khi áp dụng công thức tính thì bạn cần xác định rõ các yếu tố vào đúng vị trí, tính xong đọc lại kết quả xem hợp lý hay chưa
• Chỉ khi biết được độ dài của 2 cạnh thì mới tính được cạnh thứ 3 trong tam giác vuông
• Trường hợp tam giác không phải là tam giác vuông thì không áp dụng được Pytago 
• Nên thực hiện vẽ hình tam giác để dễ dàng gán giá trị từng cạnh, hình dung tính công thức cho chuẩn xác
• Bạn chỉ biết số đo của 1 cạnh thì không dùng được Pytago tính toán. Lúc này cần dùng hàm lượng giác là sin, cos, tan để tính. 

Cách áp dụng định lý Pytago 

Việc áp dụng định lý Pytago cũng cần phải thực hiện đúng cách thì mới có được kết quả. Bạn muốn sử dụng định lý này thì có thể tham khảo bên dưới đây để thực hiện chi tiết.

Tìm ra các cạnh của 1 tam giác vuông

Điều đầu tiên khi muốn sử dụng định lý này thì bạn cần tìm ra được các cạnh của một tam giác vuông. Các cạnh đều có vai trò riêng của nó trong một tam giác, cụ thể: 

Bước 1: Điều kiện tam giác cần tính phải tam giác vuông

Pytago là một định lý chỉ áp dụng được trong tam giác vuông. Cho nên trong khi làm bài tập hoặc nghiên cứu thì nếu không phải là tam giác vuông thì bạn áp dụng công thức khác. 

Bước 2: Làm rõ các cạnh của tam giác vuông

Bạn có thể tự vẽ ra hình tam giác vuông hoặc có sẵn hình thì bạn xác định chuẩn xác các cạnh, vị trí, vai trò trong tam giác. Cụ thể đâu là cạnh huyền, đâu là 2 cạnh của góc vuông. Cạnh dài nhất đối diện với góc vuông thì là cạnh huyền, còn 2 cạnh ngắn hơn thì là 2 cạnh góc vuông. Theo định luật này thì a, b là 2 cạnh góc vuông, c là ký hiệu cạnh huyền. 

Bước 3: Xác định cạnh huyền 

Như đã nói thì cạnh huyền là cạnh dài nhất trong tam giác vuông, ký hiệu là c. Nếu bạn biết được 2 cạnh thì bước tiếp theo là tìm cạnh còn lại. Nếu có 2 cạnh chưa rõ độ dài thì bạn cần xác định thêm 1 cạnh nữa thì mới dùng được định lý này. 

Bước 4: Thay giá trị độ dài các cạnh vào công thức

Khi biết được số đo của các cạnh biết trước thì bạn nên cho vào trong công thức cụ thể là (a^2+b^2=c^2). Bạn cần điền đúng giá trị từng cạnh vào trong công thức để tính cho chuẩn. 

Bước 5: Tính bình phương

Giải phương trình thì bạn tính ra bình phương của mỗi cạnh đã biết được. Bạn có thể để dạng số mũ rồi bắt đầu tính. Bạn phải hiểu rõ cách tính bình phương trong toán học mới tính được ra chuẩn kết quả. 

Bước 6: Tách riêng biến chưa biết sang 1 vế

Tính theo từng bước cụ thể thì bạn dùng phép toán tính số hạng trong tổng nhằm chuyển 2 số đã có số liệu sang 1 bên của công thức. Còn số chưa biết thì ở 1 bên còn lại của phương trình. Cạnh huyền c ở 1 vế để bạn tính ra hiệu số sau cùng. 

Bước 7: Giảm bình phương của 2 vế phương trình

Kết quả tìm cho thấy 2 vế của phương trình còn 1 biến bình phương vế kia lại là số xác định. Giảm bình phương 2 vế thì ra được kết quả cụ thể. 

Bước 8: Áp dụng Pitago tìm ra cạnh của tam giác vuông

Áp dụng định lý vào trong thực tế để tìm ra cạnh thì bạn cần phải xác định, hình dung rõ được hình tam giác vuông. Chẳng hạn như bạn xác định 2 đường thẳng giao với nhau hay 2 vật giao với nhau hình thành 1 góc vuông, có vật thứ 3 vắt ngang tạo thành tam giác. Lúc này thì bạn có thể vận dụng Pytago tìm ra độ dài cạnh nào đó. 

Tính khoảng cách giữa 2 điểm của mặt phẳng X-Y

Khi bạn biết được 2 tọa độ là x, y thì bạn có thể tính được ra khoảng cách giữa 2 điểm ở trong mặt phẳng X – Y. Dưới đây sẽ có chia sẻ chi tiết cho bạn cách tìm khoảng cách chuẩn xác.

Bước 1: Xác định 2 điểm cụ thể

Bạn vận dụng Pytago định lý để tính được ra khoảng cách giữa 2 điểm trong mặt phẳng X-Y. Bạn chỉ cần biết tọa độ x, y của 2 điểm nào đó bất kỳ. Bình thường thì tọa độ x, y sẽ được viết theo cặp tuần tự.

Bạn muốn tìm khoảng cách của 2 điểm thì nên xem mỗi điểm là 1 trong các góc nhọn của hình tam giác vuông. Điều này để tính số đo chiều dài của cạnh a, b rồi tính tiếp chiều dài của cạnh c chính là khoảng cách 2 điểm đó. 

Bước 2: Vẽ 2 điểm nằm trên đồ thị

Tọa độ (x, y) ở trên mặt phẳng của X-Y thì trong đó x là tọa độ ở trên trục hoành, y là tọa độ ở trên trục tung. Bạn lúc đó tìm được khoảng cách của 2 điểm mà không cần phải vẽ ra đồ thị. 

Bước 3: Tìm ra chiều dài các cạnh góc vuông

Bạn sẽ dùng 2 điểm đã biết trước của các góc ngay bên cạnh huyền. Lúc này thì bạn sẽ tìm độ dài các cạnh của góc vuông là a, b. Qua đó tính được khi sử dụng phương trình.

Bước 4: Tìm cạnh huyền bằng định lý Pytago

Ở bước này bạn sẽ áp dụng chính định lý Pytago để tìm ra cạnh huyền, là khoảng cách 2 điểm của tam giác. Phải biết được độ dài của 2 cạnh góc vuông thì mới tìm ra được cạnh huyền. 

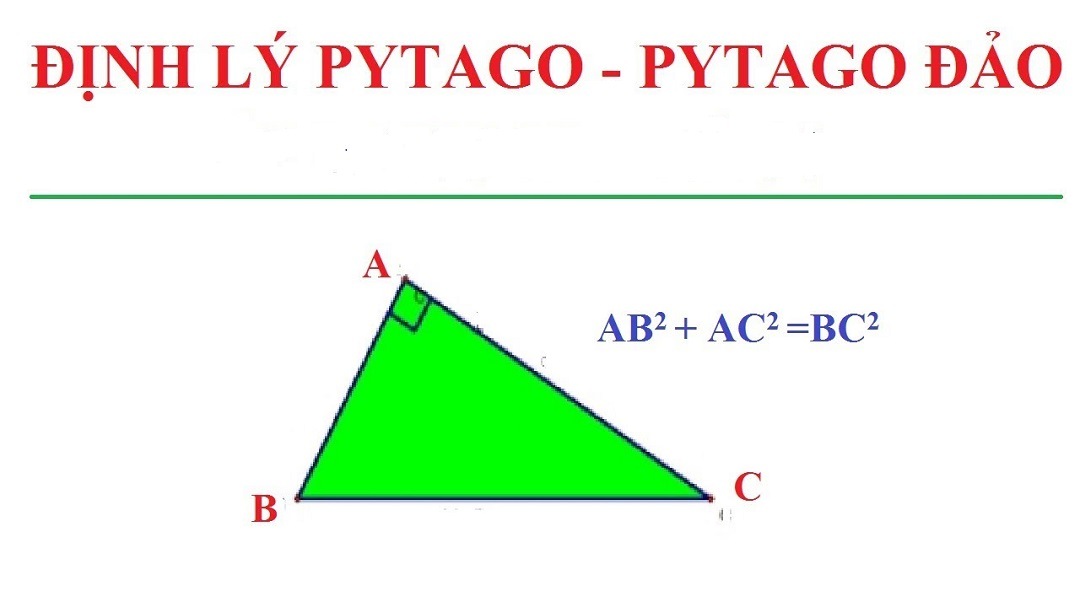
Định lý Pytago đảo 

Còn có định lý Pytago đảo trong toán học và ứng dụng trong thực tế. Cụ thể nếu 1 tam giác có bình phương của 1 cạnh bằng tổng các bình phương của 2 cạnh còn lại là tam giác vuông. 

Sử dụng Pytago định lý đảo được áp dụng phổ biến bởi mang lại hiệu quả trong thực tế. Đây là một định lý toán học quan trọng và tới bây giờ vẫn được sử dụng nhiều. 

Cách chứng minh định lý Pytago đảo chính xác 

Trên thực tế cần phải có cách chứng minh về Pytago đảo là chính xác. Như vậy việc áp dụng hoàn toàn an tâm để có được kết quả đang tìm kiếm. Cụ thể gọi ABC là tam giác với a, c là cạnh góc vuông, c là cạnh huyền, trong công thức \(a^2+b^2=c^2\). 

Dựng tiếp tam giác nữa với các cạnh bằng a, b và có góc vuông giữa chúng. Với định lý Pytago thuận thì cạnh huyền tam giác vuông thứ 2 này sẽ có c=√(a²+b²) và bằng với cạnh còn lại của chính tam giác đầu. 

2 tam giác có 3 cạnh tương ứng với chiều dài của a, b, c và 2 tam giác này bằng với nhau. Góc giữa các cạnh a, b ở tam giác thứ 1 phải là góc vuông. Chứng minh về định lý Pytago đảo có dùng chính định lý thuận. Cũng có thể hoàn toàn chứng minh định lý đảo mà không phải dùng tới định lý thuận. 

Hệ quả của định lý Pytago đảo là việc xác định một tam giác có là tam giác vuông hay không. Dưới đây là thông tin để tìm ra kết luận: 

• \(a^2 + b^2 = c^2\), tam giác này chính là tam giác vuông.
• \(a^2 + b^2 > c^2\), tam giác này là tam giác nhọn.
• \(a^2 + b^2 < c^2\), tam giác này là tam giác tù.

Lời kết

Thông tin chia sẻ từ bài viết này nêu rõ cho mọi người biết về định lý Pytago là gì, lý thuyết, cách áp dụng cụ thể làm sao cho hiệu quả và chuẩn xác. Khi bạn hiểu đúng thì có thể giải bài tập trong chương trình học hoặc thực tế có vấn đề liên quan hoàn toàn làm tốt công việc của mình.