Định lý Viet – Toán học là chuyện nhỏ với các phương trình

Định lý Viet, một trong những phát minh trong lĩnh vực toán học nhằm giúp cho những phương thức tính toán có thể được rút gọn quy trình và có kết quả chuẩn xác hơn. Chính vì thế, định lý này đã được đưa vào sách học trong các cấp để học sinh được biết đến và áp dụng trong môn toán và các môn học khác cũng như thực tế nhiều hơn. 

Tìm hiểu về sự ra đời của định lý 

Trong toán học, định lý Viet là một định lý mà nó nêu lên các mối quan hệ giữa các nghiệm của các phương trình đa thức và những kết quả liên quan đến các hệ số của nó. Định lý này do một nhà toán học người Pháp có tên là Francois Viet tìm ra. 

Đến này, định lý này đã áp dụng rất lớn vào trong lĩnh vực toán học. Các phương trình được giải mã và cho ra kết quả nhanh hơn, chính xác hơn. Quá trình giải phương trình không còn hóc búa và quá khó khăn như trước nữa. Định lý đã được chứng minh và áp dụng trên toàn thế giới trong công thức toán học. 

Tuy vậy, để có thể áp dụng được định lý, người học cần phải tìm hiểu thật kỹ và làm thật nhiều bài tập ứng dụng công thức một cách nhuần nhuyễn mới có thể thực sự hiểu rõ cũng như dễ dàng tìm ra nghiệm của phương trình. 

Tìm hiểu định lý Viet trong lĩnh vực toán học

Định lý Viet được áp dụng rất rộng rãi và phổ biến trong môn toán. Đặc biệt là trong những bài tập giải phương trình khó. Do đó, việc áp dụng định lý của nhà toán học Vi-et sẽ giúp cho những bài tập toán trở nên không có gì khó khăn nữa. 

Trong môn toán, khi áp dụng định lý của nhà toán học Vi-et vào việc giải phương trình, các nghiệm sẽ được tìm ra cùng với hệ số của phương trình cũng được hiện diện nhanh chóng. Định lý như một lối tắt trong việc tìm nghiệm của các phương trình đa thức. Chính vì thế, trong toán học, định lý này là một phát minh vô cùng vĩ đại và được toàn bộ thế giới công nhận, sử dụng. 

Ngoài lĩnh vực toán học, định lý này còn có thể áp dụng cho các môn học tính toán khác, đặc biệt là vật lý. Nó cũng được ứng dụng rất nhiều trong đời sống hàng ngày, nhưng lúc cần tính toán nhanh thì sử dụng định lý là một phương pháp hiệu quả và nhanh chóng nhất. 

Sử dụng định lý Viet trong phương trình 

Định lý Viet do nhà toán học Vi-et tìm ra được sử dụng khá đa dạng trong các bài tập giải phương trình của môn toán học. Những dạng phương trình có thể áp dụng một cách dễ dàng và phổ biến nhất chính là phương trình bậc 2, bậc 3 và các phương trình đa thức. 

Giải phương trình bậc 2 bằng định lý Viet

Ta có phương trình bậc 2 dưới dạng công thức tổng hợp như sau: ax mũ 2+bx+c. Ta sẽ có nghiệm là x1 và x2. Từ định lý của nhà toán học Vi-et, người áp dụng có thể tìm ra hai nghiệm của chúng qua công thức sau: x1+x2= -b/a và x1.x2=c/a.

Từ công thức trên, ta còn suy ra được hệ quả của định lý. Nếu ba hệ số a, b, c của phương trình có tổng bằng 0, thì kết quả của phương trình sẽ dễ dàng hơn. Bởi trong hai nghiệm của phương trình sẽ có nghiệm thứ nhất x1 = 1 và nghiệm còn lại được gọi là x2 sẽ có kết quả từ phép tính c/a. 

Nếu như kết quả của ba hệ số trong phương trình bậc hai qua phép tính a- b + c=0 thì nghiệm đầu tiên của phương trình đó x1= -1 và nghiệm còn lại sẽ có kết quả là -c/a. Đây chính là hệ quả của định lý thuận cho phương trình bậc hai. 

Dựa vào hệ thống của phương trình được viết tắt là a, b và c cũng có thể tìm ra nghiệm x1 của phương trình. Chính  vì vậy, trước khi bắt tay vào giải một phương trình bậc hai nào đó, người làm bài hãy đọc kỹ và cộng các hệ số với nhau trước để có thể rút ngắn thời gian tính toán cũng như áp dụng được hệ quả của định lý một cách tốt nhất. 

Giải phương trình bậc 2 một ẩn bằng định lý Viet

Với phương trình bậc hai đã cho và có điều kiện rằng a là một hệ số khác 0. Để giải phương trình này ta cần tính den ta với công thức hệ số b mũ hai trừ đi cho 4 lần hệ số a nhân c. Từ kết quả của đen ta, kết quả của phương trình sẽ được tìm ra. 

Nếu đen ta có kết quả nhỏ hơn 0, đồng nghĩa với việc phương trình đã cho vô nghiệm. Nếu kết quả của phép tính đen ta bằng 0, phương trình có hai nghiệm tuy nhiên x1=x2 và chúng sẽ được tính bằng -b/2a. 

Nếu đen ta được tính ra và kết quả lớn hơn 0, thì phương trinh fđx cho sẽ có hai nghiệm khác biệt nhau và được tính bằng hệ công thức kép x1 + x2 = -b/a và x1 nhân x2 = c/a. Dựa vào hệ kép này kết quả x1 và x2 sẽ được tìm ra dễ dàng. 

Giải phương trình bậc 3 bằng định lý Viet 

Trong phương trình bậc ba có công thức: a.x mũ 3 cộng hệ số b nhân x mũ 2 cộng hệ số c nhân x cộng hệ số d với điều kiện hệ số a không phải là 0, ta sẽ có ba nghiệm tương ứng với số bậc của phương trình, đó chính là x1, x2, và x3. Nhiệm vụ của người giải phương trình chính là tìm ra kết quả chính xác cho ba nghiệm bằng cách sử dụng định lý. 

Áp dụng định lý Viet vào bài toán, ta sẽ tìm ra được ba nghiệm lần lượt bằng những công thức như sau: tổng của ba nghiệm x1+ x2 + x3= -b/a; x1.x2+x2.x3+x1.x3 = c/a; x1.x2.x3 = d/a. Từ ba phương trình kép này, người giải sẽ tìm ra được lần lượt các nghiệm đang bị ẩn và cho ra đáp án chính xác của phương trình. 

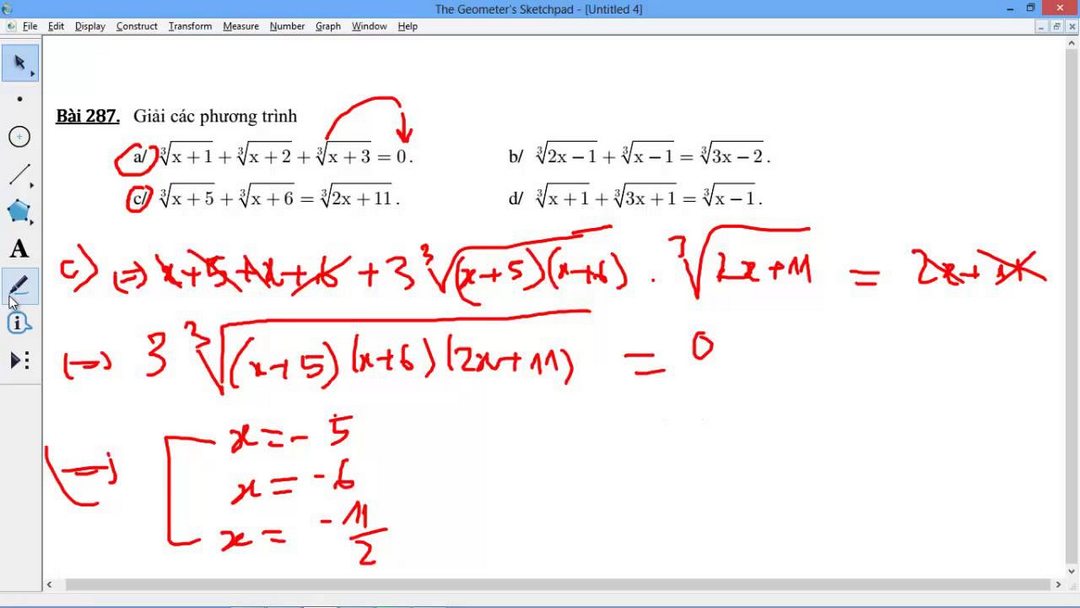
Giải phương trình đa thức bất kỳ bằng định lý Viet

Không chỉ có phương trình bậc 2 và bậc 3 mới có thể áp dụng được định lý Viet trong tính toán Các phương trình đa thức khác đều có thể áp dụng. Tuy nhiên, công thức tính toán sẽ có chút phức tạp hơn bởi đó là những phương trình có nhiều hệ số, có số mũ cao và tăng giảm rất nhiều. Thường trong các phương trình đa thwucs đó sẽ có nhiều hơn 2 nghiệm cho người giải cần tìm ra. 

Áp dụng định lý Viet, ta sẽ có công thức tìm ra các nghiệm như sau. Đầu tiên sẽ nhân toàn bộ vế phải với nhau, tức là nhân hệ số -a cùng với các nghiệm đang bị ẩn được viết tắt là x1, x2, x3, … cho đến xn. 

Phương trình đa thức là một phương trình rất khó giải quyết và để tìm ra chuẩn xác tất cả các nghiệm đều cần quá trình phức tạp. Định lý Viet ra đời đã hỗ trợ rất lớn trong việc giải phương trình, đặc biệt là các dạng bài tập có cấp độ nâng cao.

Áp dụng định lý vào lĩnh vực toán học

Không chỉ dùng để giải phương trình trong các dạng bài tập có ẩn và các phương trình đa thức nhiều bậc. Trong toán học, định lý Viet còn được áp dụng trên nhiều phương diện khác nhau. Tiếp tục theo dõi để biết thêm thông tin bổ ích về các ứng dụng của định lý. 

Dùng định lý cho bất đẳng thức 

Định lý Viet thường xuyên được áp dụng trong việc chứng minh các bất đẳng thức, tuy nhiên, nó chính đóng vai trò trung gian, là cầu nối để giúp việc chứng minh dễ dàng hơn. Bởi trong các bài toán chứng minh bất đẳng thức, đề bài thường xuyên đưa ra các dữ liệu thiên về những phép tổng hoặc tích. 

Và thật tình cờ, định lý Viet lại là một định lý phù hợp để chỉ ra mối liên hệ, sự tương ứng giữa các hệ số nhờ vào tổng và tích của phép tính. Chính vì thế, người dùng có thể sử dụng định lý này để chứng minh các bất đẳng thức, tam thức hoặc một số phép biến đổi có tổng tích tương đương. 

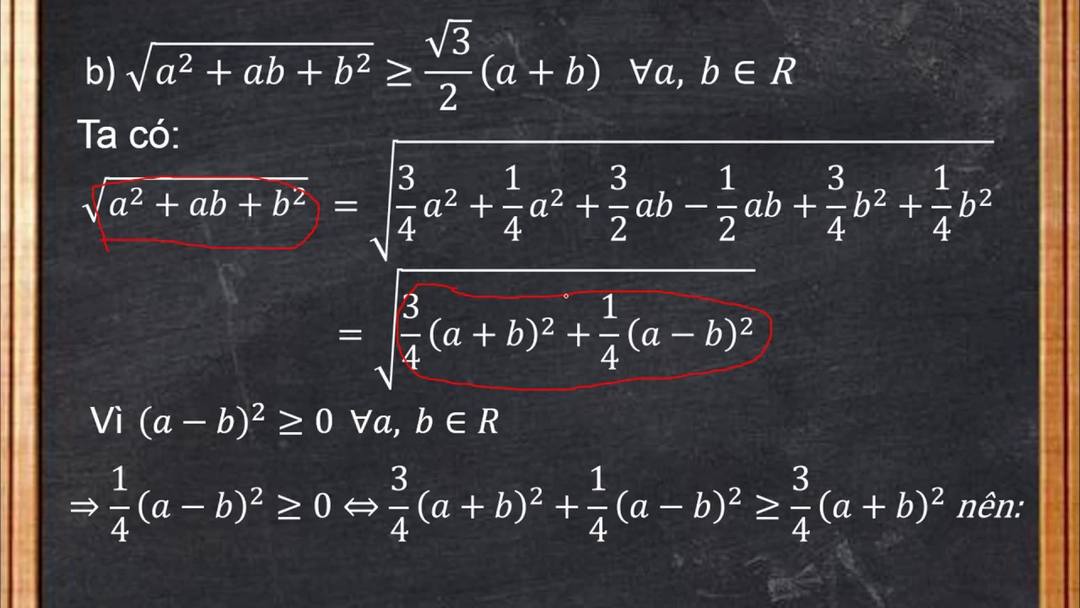
Tính cực trị cho hàm số đã cho 

Tính cực trị của một hay nhiều hàm số đã cho trước là dạng bài toán rất phổ biến trong chương trình học. Đặc biệt dạng toán này đang được áp dụng rất nhiều trong các đề thi các kỳ cũng như đề thi đại học quốc gia. Vì thế, cách giải đề sao cho nhanh nhất, thuận tiện nhất là điều hầu hết các bạn học sinh đang quan tâm. 

Và định lý này sẽ là một trong những giải pháp rất tốt để áp dụng công thức, tính ra cực trị cũng như vẽ được biểu đồ thể hiện sự lên xuống, nghịch đảo của hàm số mà đề bài đưa ra. Nhờ vào định lý, các tọa độ của cực điểm sẽ được tìm ra nhanh chóng hơn rất nhiều, rút ngắn thời gian làm bài cho thí sinh. 

Sử dụng định lý để giải toán tiếp tuyến 

Hầu hết tất cả các bài tập về tiếp tuyến sẽ có liên quan đến các giao điểm, thể hiện đường cong và các đường thẳng. Trong dạng toán này, người giải cần phải tìm ra tọa độ tiếp xúc của các đường giao nhau, bởi đó chính là nghiệm của các phương trình. 

Từ tọa độ tiếp xúc, người giải hãy thành lập các phương trình phù hợp và đưa về công thức của định lý Viet để giải bài tập nhanh gọn nhất và tìm câu trả lời cho bài toán. Ở dạng bài tập này, các kỹ năng nhẩm nghiệm phương trình cần được phát huy tối đa. 

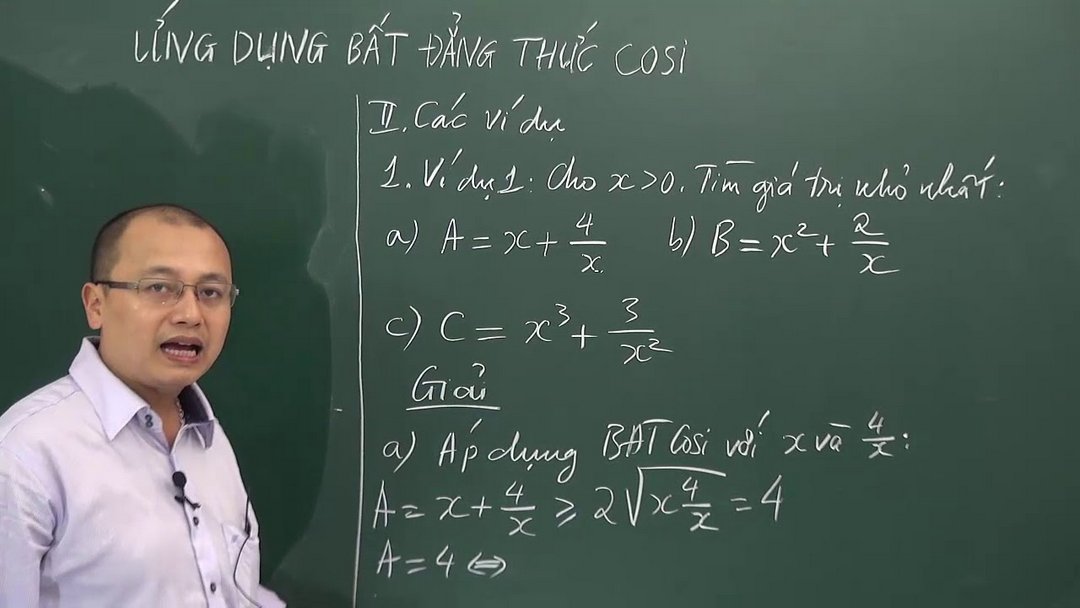
Áp dụng trong bài tập có 2 đồ thị giao nhau 

Đây là dạng bài tập cần người giải viết phương trình tọa độ hoành điểm. Từ phương trình, học sinh hãy áp dụng định lý Viet có sẵn để có thể hiện được biểu thức mà đề bài đã cho. Sau đó dựa vào hệ số của phương trình, hãy đưa ra những nhận xét, đáng giá mà phương trình hiểu thị. 

Đây cũng là một dạng bài xuất hiện rất nhiều trong bộ đề cương cũng như đề thi tốt nghiệp quốc gia hàng năm. Vì vậy, chọn phương pháp giải tốt nhất, hiệu quả nhất sẽ giúp cho thí sinh vừa có thể hoàn thành bài vừa nhanh vừa chính xác. 

Ngoài việc áp dụng rất nhiều trong các đề bài của môn toán học như đã kể trên, vẫn còn rất nhiều loại bài tập cần đến sự trợ giúp của định lý này. Vậy nên, việc am hiểu và vận dụng tốt định lý sẽ giúp cho người học phần nào cải thiện môn toán hơn rất nhiều. 

Kết luận 

Định lý Viet được áp dụng rộng rãi trên toàn thế giới, đặc biệt là trong môn toán. Nhiều dạng bài tập chỉ cần hiểu về định lý thì bạn đã tìm ra được hướng đi và hướng giải quyết tốt nhất. Hiểu được định lý và áp dụng tốt nó sẽ giúp cho môn toán không còn khó khăn và nhàm chán nữa.