Định lý Talet và những kiến thức bổ ích cần được biết

Định lý Talet được xem là một trong những khái niệm toán học hết sức quan trọng từ cổ đại, cận đại và cả hiện đại. Nếu là một người từng ngồi trên ghế nhà trường, được học toán thì ít nhất 1 lần từng gặp qua định lý này, không chỉ là một công thức toán thông thường, dạng định lý này có nhiều hiệu quả trong việc tính toán, cũng như khả năng ứng dụng trong hình học không gian.  

Giới thiệu định lý Talet

Định lý Talet có thể được hiểu là một dạng định lý có tầm ảnh hưởng cực lớn trong hình học không gian, nó được đặt theo tên nhà toán học người Hy Lạp, ông Thales. Nói sơ qua một chút về cha đẻ của định lý, Thales không chỉ là nhà toán học mà ông còn là một triết gia nổi tiếng, ngoài ra người ta còn biết đến việc ông chính là thầy dạy của  Pythagoras, người sau này cũng đã phát minh ra định lý Pythagoras.

Cha đẻ của định lý Talet sống trong khoảng thời gian từ 635 TCN– 578 TCN, có nhiều tài liệu ghi chép rằng ông Thales sống thọ đến 90 tuổi. Nếu xét theo trường phái, ông thuộc hệ tư tưởng triết lý Ionian, trường phái Milesia và theo dạng chủ nghĩa tự nhiên. Mặc dù định lý toán học của Thales gặp phải nhiều ý kiến trái chiều nhưng trải qua thời gian dài đấu tranh, công chúng cũng đã hiểu được hàm ý.

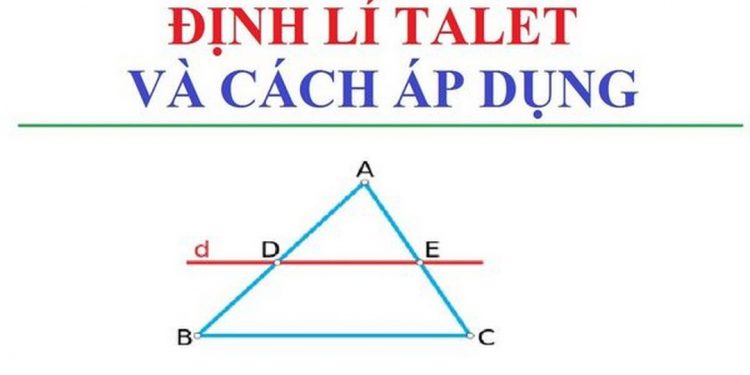
Định lý này được phát biểu đầy đủ và chính xác như sau, nếu như có một đường thẳng nằm song song so với 1 cạnh của tam giác đó và cắt 2 cạnh còn lại thì hệ quả nó sẽ định ra trên 2 cạnh đó những đoạn thẳng tương ứng tỉ lệ đang có. Dạng định lý này rất nổi tiếng, có trong gần như tất cả các sách giáo khoa toán học của nhân loại, ở Việt Nam, dạng định lý này xuất hiện trong sách giáo khoa toán lớp 8.

Hệ quả của định lý Talet trong toán học

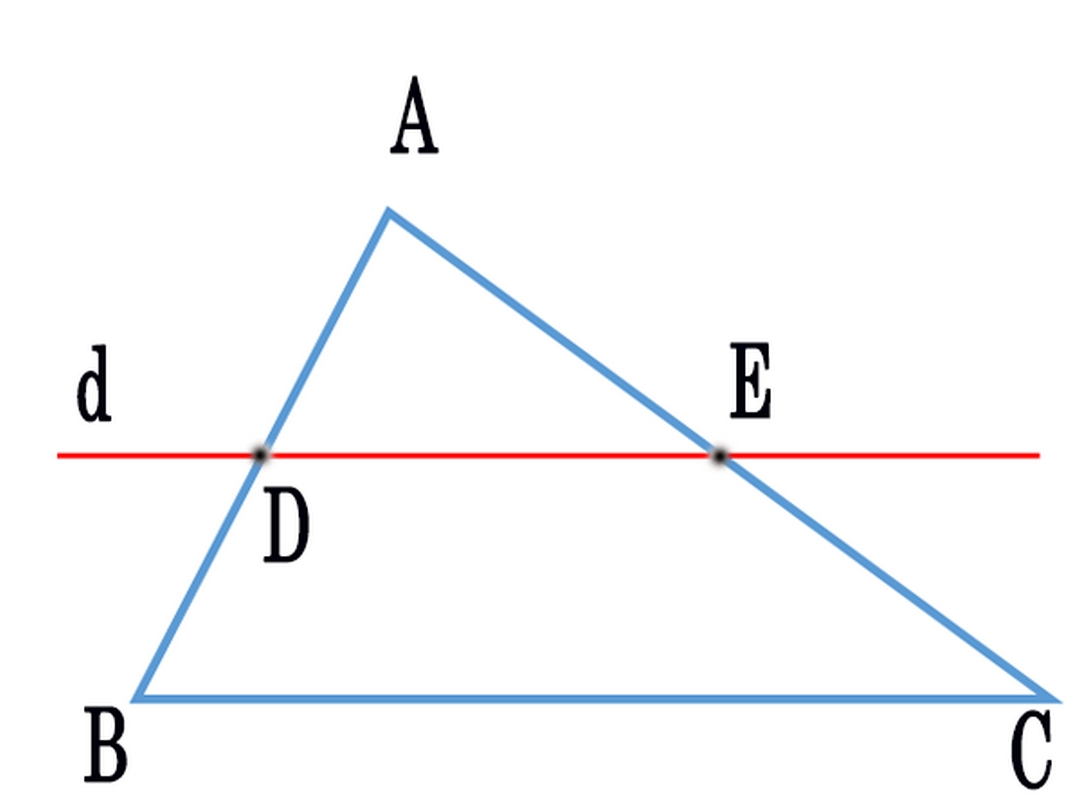
Để có thể hiểu rõ hơn về định lý Talet, người học cần biết được những hệ quả chung có nó. Hệ quả đầu tiên đó chính là nếu một đường thẳng cắt hai cạnh hoặc có thể cắt phần kéo dài của hai cạnh của một tam giác và song song với cạnh còn lại thì lúc này nó sẽ tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho trước đó.

Điều đó có thể hiểu rằng, nếu ví dụ ta cho tam giác ABC, có B’C’ song song với BC thì lúc này AB’/AB=AC’/AC=B’C’/BC. Hệ quả này luôn đúng và được áp dụng trong nhiều bài toán khác nhau, ở một số trường hợp hình học khác, người làm bài cần tính toán và áp dụng công thức một cách phù hợp.

Ngoài hai hệ quả trên thì trong định lý Talet còn có một hệ quả nữa, nó còn được biết đến như là một dạng định lý mở rộng. Trong đó một khi trường hợp ba đường thẳng đồng quy thì sẽ chắn trên 2 đường thẳng song song những cặp đoạn thẳng tỉ lệ, hệ quả này ít khi xuất hiện nhưng cũng là cách giải phù hợp ở các bài toán có độ khó trung bình hoặc cao.

Ứng dụng của định lý Talet 

Định lý Talet cũng có nhiều ứng dụng trong hầu hết nhiều những bài toán hình học khác nhau. Nếu như là một người ham giải toán hình bạn sẽ thường gặp và áp dụng chúng trong các bài toán tính chu vi của đoạn thẳng, hình học, đôi khi sẽ cần phải chứng minh các đường thẳng có song song với nhau hay không, chi tiết hơn như sau.

Tạm gác lại những dạng toán của định lý này, không chỉ trên sách vở, ngoài đời công thức toán học trên được ứng dụng rất rộng rãi, trở thành một công cụ không thể thiếu. Chúng phát huy tác dụng khi đo đạc những kích thước quá lớn và không tự tay con người đo được. Cụ thể nó được áp dụng trong 2 trường hợp điển hình sau đây.

Đo khoảng cách

Định lý của Talet được áp dụng để đo đạc khoảng cách ở giữa 2 bờ sông, không cần phải tính toán quá nhiều, chỉ cần áp dụng công thức có sẵn. Tỷ lệ chính xác của cách làm này là 97%, không cần khiến người đo phải đi từ bờ sông này sang bờ sông bên kia, cách làm này cũng đã được dùng vào thời cổ đại với độ sai số rất thấp.

Không những thế, nhờ việc áp dụng định lý nên việc đo khoảng cách của những con đường trở nên đơn giản hơn hẳn. Có thể thấy mặc dù chúng là những bài toán cổ xưa nhưng đến thời điểm hiện tại vẫn có độ chính xác cực tốt. Hãy ứng dụng ngay định lý này để tính toán về khoảng cách nhanh chóng nhất bạn nhé. 

Đo chiều cao

Định lý của Talet còn được áp dụng để đo cả chiều cao của các vật, tuy nhiên nó chỉ phát huy tác dụng trong điều kiện ánh sáng mặt trời ở mức tốt. Người ta thường đo cây cối, nhà cửa với các thước đo chuyên dụng nhưng nếu áp dụng định lý trên độ chính xác sẽ khá tốt. Ví dụ để đo chiều cao của một cái cây nhưng không dùng thước hay trèo lên cây mà người ta chỉ cần đo đổ bóng của cây đó.

Như vậy nhờ vào định lý trên, con người đã có nhiều phương án và tiết kiệm thời gian hơn trong việc đo khoảng cách, đo chiều cao,…. Cho đến thế kỷ hiện tại, chúng ta có thể thấy định lý được sử dụng trong cả chế tạo máy móc, thiên văn học, thiết kế, xây dựng…

Định lý Talet trong hình thang

Định lý Talet có thể được áp dụng trong cả hình thang, theo định nghĩa thì  định lý này được phát biểu như sau. Trong một hình thang bình thường, luôn có một đường thẳng song song cùng 2 cạnh đáy bên cạnh đó cũng sẽ đồng thời cắt 2 cạnh bên của hình thang, lúc này thì sẽ định ra tại 2 cạnh bên đó với những đoạn thẳng có tỷ lệ tương ứng với nhau.

Định lý Talet trong hình tam giác

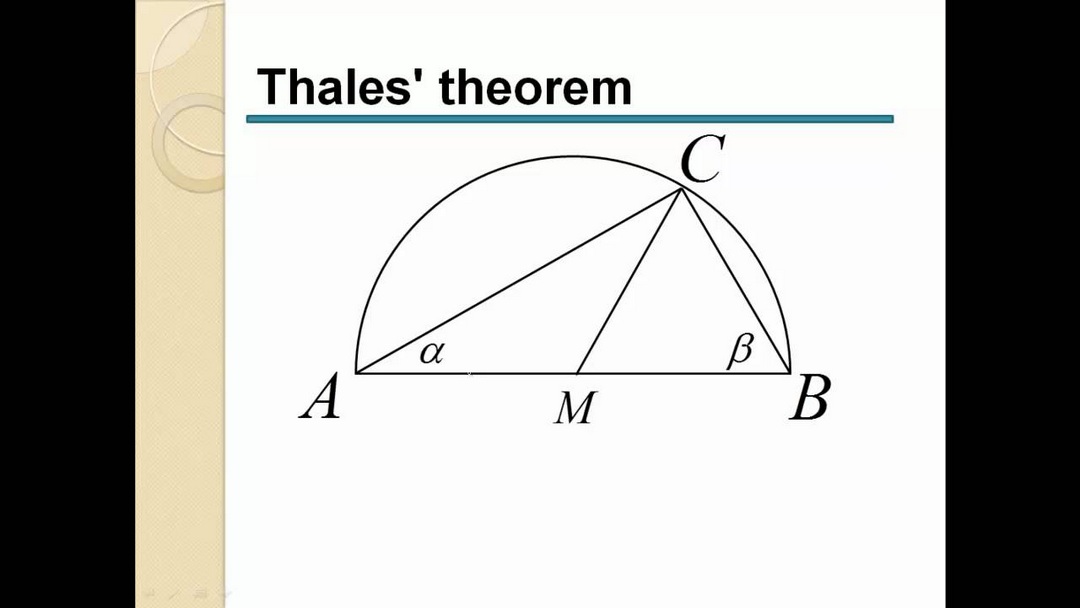
Qua những kiến thức bên trên có lẽ các bạn cũng phần nào hình dung và hiểu được định lý Talet trong hình tam giác. Nó được coi là một định lý mang tính chất 2 chiều, trong đó gồm chiều thuận và chiều đảo ngược. 

Hiểu đơn giản trong một tam giác bình thường, nếu như một đường thẳng cắt 2 cạnh của tam giác đó và cũng  định ra trên 2 cạnh được cắt ra những đoạn thẳng có tỷ lệ tương ứng với nhau thì lúc này đường thẳng đó sẽ song song với cạnh còn lại. Cũng như đã đã đề cập trong phần trước, trong tam giác định lý này áp dụng với các dạng toán và 3 hệ quả khác nhau.

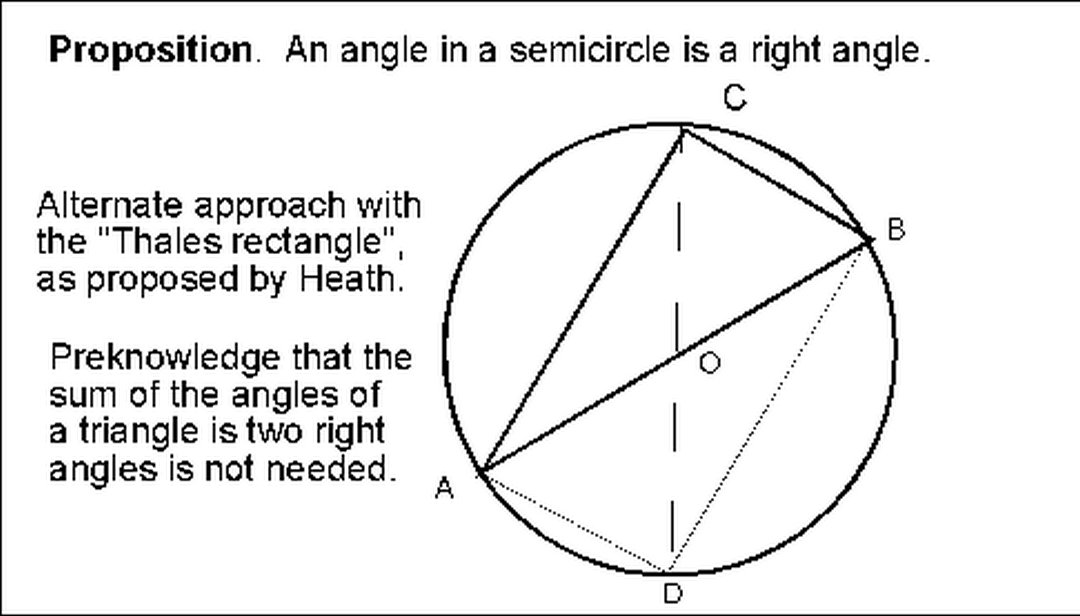
Áp dụng định lý Talet trong các hình không gian

Ngoài ra dạng định lý này còn được áp dụng trong cả hình không gian, nó được phát biểu như sau. 3 mặt phẳng song song trong không gian sẽ chắn trên trong số 2 đường thẳng những đoạn thẳng có tỷ lệ tương ứng nhau, không những thế người ta còn phát biểu cả định lý đảo của Talet.

Các dạng toán thường gặp

Từ khi bắt đầu làm quen với định lý, tức là năm học lớp 8, bạn sẽ gần như gặp thường xuyên các bài toán hình học cần áp dụng công thức này. Nó chủ yếu gồm 2 dạng như sau:

Dạng toán số 1 trong định lý Talet

Dạng toán này cần tính độ dài của đoạn thẳng, tính luôn cả các tỉ số, chu vi hoặc diện tích. Những dạng giải toán kiểu như vậy sẽ luôn được áp dụng định lý Talet vào để giải tốt nhất có thể, bên cạnh đó cũng cần quan tâm đến hệ quả của định lý và tỉ số đoạn thẳng.

Nếu nói về định lý, trong trường hợp nếu một đường thẳng nó song song với một cảnh của tam giác và cũng cắt luôn hai cạnh còn lại thì sẽ có thể định ra được những đoạn thẳng tương ứng tỉ lệ. Khi ứng dụng theo cách này cần có khả năng quan sát tốt, luôn để ý tới hệ số đường thẳng ra sao.

Dạng toán số 2 trong định lý

Đây cũng chính là một dạng toán gặp khá nhiều, đặc biệt là trong chương trình hình học phổ thông, ôn thi đại học, nó cũng có thể áp dụng định lý Talet. Đó chính là việc chứng minh các đường thẳng song song và chứng minh đẳng thức trong hình học. Bạn cần thông minh áp dụng định lý đảo của Talet hoặc định lý thuận tùy trường hợp.

Nói thêm về định lý đảo Talet, nó có thể được hiểu đơn giản như sau. Nếu như một đường thẳng cắt hai cạnh trên cùng một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó thì lúc này sẽ song song so với hai cạnh. Nên nhớ định lý Talet đảo chỉ áp dụng tam giác khác hoàn toàn định lý thuận.

Một số thông tin khác về định lý của Talet

Nếu như ở nước ta hay áp dụng định lý này để đo chiều cao hoặc khoảng cách thì bên một số quốc gia Châu Âu, họ còn vận dụng chúng vào trong các khâu kỹ thuật công trình. Chẳng hạn như chế tạo gạch & sơn, giúp đảm bảo rằng nó theo tỷ lệ đúng nhất.

Quân đội của các nước NATO và một số quốc gia khác trên thế giới cũng hay áp dụng định lý này nhằm cải thiện tính chính xác của các đầu đạn hạt nhân. Đo khoảng cách của các điểm nổ, cùng với đó nghiên cứu tính hiệu quả trong kỹ thuật quân sự.

Nhờ vào định lý, người ta cho rằng tâm trí trong vũ trụ là thượng đế, và tất cả đều được trời phú cho linh hồn và linh hồn cũng có sức mạnh di chuyển thần thánh của nó lan tỏa khắp mặt nước ( trích lời của Talet).

Không dừng lại ở đó, một số nhà nghiên cứu còn cho rằng Talet có nhiều ảnh hưởng trong thực tế của tỷ trọng trực tiếp. Chẳng hạn như việc tính chi phí của một đối tượng so với số lượng đối tượng đã mua, tính số thu nhập của một công nhân mỗi ngày, mức tiêu thụ xăng dầu và quãng đường đã đi hay tuổi và chiều cao của một người bình thường.

Tổng kết

Như vậy, sau bài viết trên, hy vọng mọi người cũng đã có được những cái nhìn tổng hợp nhất về định lý Talet cũng như hiểu được các hệ quả, ứng dụng các dạng toán sử dụng định lý. Là một trong những lý thuyết quan trọng nhất trong toán học nếu bạn không nắm bắt sẽ là một điều rất thiệt thòi.