Định lý Cosin – Những kiến thức phổ thông cần phải biết

Định lý Cosin có thể nói là một trong những công thức toán học, định lý toán học kinh điển nhất mọi thời đại, khi nó có thể mang đến những áp dụng to lớn cả trong khía cạnh toán học và đời sống. Kiến thức về định lý này đối với thế hệ các bạn học sinh, đặc biệt là học sinh trung học cực kỳ quan trọng. Nó đóng góp ý nghĩa to lớn trong việc hình thành tư duy và sự thông minh toán.

Khái quát về sự ra đời của định lý cosin trong toán học

Như bao định luật toán học khác, định lý cosin là điển hình cho sự kế thừa và phát triển qua thời gian. Chúng ta đã nhắc về định lý Pitago như một công thức toán học đầu đời, một công trình nổi tiếng của tam giác vuông. Nhưng khi nhắc về định lý cos này, nó như sự kế thừa và phát triển hoàn hảo mà công trình của Pitago còn dang dở.

Nếu công trình của Pitago trong tam giác vuông chỉ ra mối quan hệ của các cạnh trong một tam giác vuông, một tam giác đặc biệt, một trường hợp đặc thù. Nhưng đối với các tam giác khác thì sao? Làm sao chúng ta có thể tính được góc của những tam giác không vuông, không cân? Làm sao để tìm được chiều dài các cạnh.

Định lý Cosin được phát triển bởi thiên tài toán học, số học người Iran- Al Kashi. Chính vì vậy, khi nhắc về định lý này, chúng ta thường nói ngắn gọn: định lý Cos hoặc đầy đủ: định lý Al Kashi. Công trình này chính thức hoàn thành và công bố từ giai đoạn thế kỷ XIV. Đến nay, nó vẫn được áp dụng rộng rãi và cực kỳ phổ biến.

Như vậy, nói về nguồn gốc sự ra đời thì chúng ta có thể khái quát ngắn gọn như vậy. Tiếp theo, hãy tìm hiểu sang nội dung liên quan đến định lý cos trong một tam giác thường được áp dụng như thế nào?

Về định lý Cosin trong một tam giác thường

Như đã nói, sự hình thành của định lý Cos là kế thừa và khắc phục hoàn hảo các tồn tại trong định lý Pitago để lại. Điều này cho thấy rằng trong một tam giác thường, định lý Cos cũng được áp dụng hiệu quả và không hạn chế. Tiếp theo đây, hãy tìm hiểu về cách phát biểu của định lý Cos trong tam giác thường.

Về cơ bản, nó được phát biểu như sau: trong một tam giác bất kỳ, bình phương của một cạnh luôn bằng tổng bình phương 2 cạnh đối diện với nó trừ đi 2 lần tích của 2 cạnh đối diện và cos góc được tạo bởi chúng. Bạn hãy nhớ lấy công thức này vì nó có ý nghĩa quan trọng trong sự phát triển của toán học sau này.

Về công thức, nó có dạng như sau: a2= c2 + b2 – 2abcosA. Với a là cạnh cần tìm, ta có c và b là 2 cạnh đối diện cạnh a trong một tam giác. Góc A: góc được tạo thành bởi 2 cạnh này, được gọi lòa góc đối diện cạnh a nên ta có CosA. Vậy tương tự thì bạn cũng có thể tìm thấy công thức ngược lại cho các cạnh c và b tương tự trong định lý Cos.

Những khái quát ban đầu này mà Al Kashi đã tìm ra trong công trình của mình rất hoàn thiện. Một đẳng thức toán học, một định lý toán học luôn sẽ được khai phá liên tục. Điều đó hình thành nên những hệ quả và khẳng định sự chính xác, vững chắc của công trình nghiên cứu ban đầu. 

Hệ quả của định lý Cosin

Tiếp theo, chúng ta sẽ nói về những hệ quả của định lý Cosin. Những hệ quả này bao gồm các công thức được tạo ra từ việc khai phá định lý này cũng như những ứng dụng thiết thực trong đời sống thực tế. Hãy khám phá ngay sau đây.

Về công thức hệ quả định lý Cosin

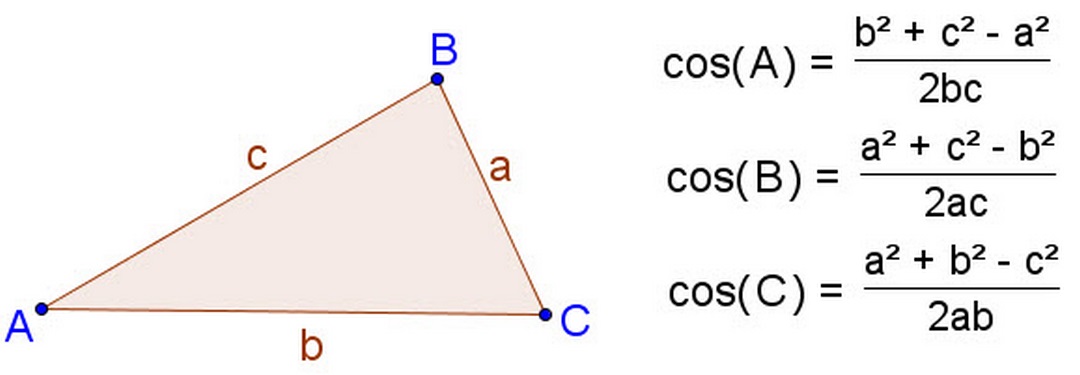
Hệ quả định lý Cos thể hiện qua các công thức toán học. Nếu bạn biết độ dài của 3 cạnh thì chúng ta sẽ tính được số đo của các góc trong một tam giác. Tương tự với một góc cho trước cùng với chiều dài 2 cạnh thì chúng ta cũng có thể tìm ra được chiều dài cạnh còn lại. Công thức được phát biểu dưới dạng: Cos A = (b2 + c2 – a2)/2bc.

Cũng tương tự thì bạn cũng có thể suy ra cos của các góc B và C nếu biết chiều dài của các cạnh. Công thức này chính xác tuyệt đối, cho nên được áp dụng nhiều và rộng rãi trong cả mặt toán học, đời sống, lập trình công nghệ cũng rất cần thiết. 

Hệ quả của định lý Cos chưa dừng lại ở đó, nó cũng có công dụng trong việc giúp chúng ta tìm ra chiều dài đường trung tuyến trong một tam giác. Đường trung tuyến là đường kẻ từ đỉnh bất kỳ đến trung điểm cạnh đối diện. Bạn có thể tìm thấy chiều dài đường trung tuyến qua hệ quả định lý Cos như sau: Ma2 = [2( b2 + c2 ) – a2] / 4

Ma tức đường trung tuyến nối từ đỉnh A đến cạnh đối diện của nó. Tương tự Mb tức chiều dài đường trung tuyến bắt đầu từ đỉnh B và Mc cũng tương tự, chiều dài đường trung tuyến bắt đầu từ đỉnh C. Như vậy,  bạn cũng có thể áp dụng tương tự để tìm ra chiều dài trung tuyến của các đường Mb và Mc.

Về ứng dụng trong mặt thực tiễn

Định lý cosin và các hệ quả của nó còn có ý nghĩa luận to lớn trong toán học. Áp dụng công trình này, người ta dễ dàng thực hiện trong toán đo đạc, khi việc đo đạc phổ thông theo các cách truyền thống quá mất thời gian. Thay vào đó, chỉ với góc được tạo ra từ 2 cạnh thì chúng ta sẽ biết được chiều dài của chúng.

Điều này đã được áp dụng từ sau thế kỷ XIV, vậy nên, có thể nói dù công nghệ có phát triển thì vẫn có những ý nghĩa nhất định mà định lý này mang lại. Ngoài ra, ngày nay công nghệ và lập trình phát triển, việc áp dụng định lý cos trong lập trình cũng có thể tạo ra nhiều bài toán hay, giải quyết các vấn đề mang tính thực tiễn lớn.

Cuối cùng, định lý Cosin được áp dụng trong nhiều trường đại học, trường trung học và trở thành kiến thức nền tảng của các bạn học sinh. Bởi vậy mà nó có ý nghĩa to lớn trong hình thành tư duy toán học và giúp các bạn thông minh hơn.

Chứng minh sự chính xác của định lý Cos

Việc chứng minh định lý Cos đã được thực hiện rất nhiều hiện nay, việc chứng minh tính chính xác của một định lý hay một công thức toán học nào đó giúp cho các bạn có thể dễ dàng làm quen và ghi nhớ nhanh chóng. Hệ thống tri thức sẽ được đón nhận một cách linh hoạt nhưng lâu bền.

Hiện nay, các đẳng thức, định lý, tính chất hay các công thức một số các bạn sử dụng đều là thuộc dạng thừa nhận không chứng minh. Sự thừa nhận là chính xác nhưng nó chỉ dừng ở mức ứng dụng, còn việc chứng minh tính chính xác của nó sẽ giúp ích trong việc ứng dụng và làm bài tập. Giúp các bạn nhận diện ra dạng toán cần định lý Cos và giải quyết bài toán dễ dàng.

Đối với việc chứng minh sự chính xác của các đẳng thức hay định lý này rõ ràng mang đến sự hiểu biết và nhớ lâu hơn cho các bạn. Sau đây, hãy chứng minh tính chính xác của định lý Cos ngay nhé.

Tổng hợp các công thức của định lý Cosin

Cuối cùng, để giúp các bạn ôn lại các công thức và đẳng thức cần thiết trong định lý Cosin, chúng ta hãy nhắc lại tất cả các công thức cần thiết cho các bạn. Hãy nắm những công thức này để vận dụng định lý một cách trơn tru, chính xác nhất. 

Các công thức liên quan

Giả thiết: Cho tam gia ABC với A là góc được tạo bởi cạnh ac và cạnh ab, B là góc được tạo bởi cạnh bc và ba, C là góc được tạo bởi cạnh cb và ca. Lần lượt các cạnh trong tam giác là ab, ac và cb. Ta có:

• Về định lý Cosin: Ta có, trong tam giác vuông thì sẽ có cos góc vuông bằng 1. Vậy nó sẽ luôn đúng khi tam giác đang được xét trong các bài toán là tam giác vuông.

a2= c2 + b2 – 2bccosA

b2= c2 + a2 – 2accosB

c2= a2 + b2 – 2abcosC

• Về hệ quả định lý Cos: 

Cos A = (b2 + c2 – a2)/2bc. 

Cos B = (a2 + c2 – b2)/2ac.

Cos C = (b2 + a2 – c2)/2ab.

• Về hệ quả của công thức đường trung tuyến

Ma2 = [2( b2 + c2 ) – a2] / 4

Mb2 = [2( a2 + c2 ) – b2] / 4

Mc2 = [2( b2 + a2 ) – c2] / 4

Trên đây tổng hợp toàn bộ các công thức liên quan đến định lý Cosin cơ bản dành cho các bạn học sinh trung học. Để có thể làm quen nhiều hơn, các bạn nên làm các dạng toán liên quan, mặc dù ban đầu sẽ khá khó khăn.

Nhưng việc nắm vững các công thức này sẽ giúp các bạn đạt được điểm cao trong các kỳ thi, tạo cho các bạn những kiến thức vững chắc sau này. Vậy nên, đừng ngại tìm hiểu, toán học là một kho tàng quý báu mà sẽ cho các bạn rất nhiều bất ngờ nếu chịu tìm tòi và nghiên cứu.

Dạng toán dùng định lý Cosin

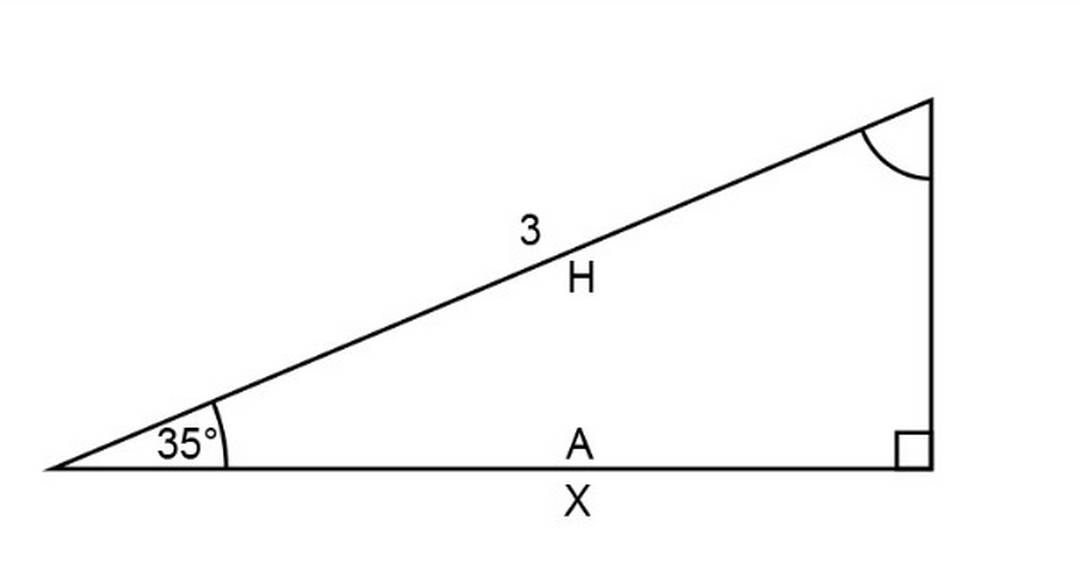
Hiện nay, có một số dạng toán được ứng dụng với hàm cos. Khi học ở bậc trung học cơ sở, các bài toán sẽ dễ hơn nhưng nó sẽ tăng dần theo cấp học. Khi học đến trung học phổ thông, các dạng toán còn mở rộng hàm cos sang rút gọn biểu thức. Điều này sẽ thuộc các câu hỏi nâng cao trong các bài thi và kiểm tra.

Phổ biến hiện nay đối với các bạn trung học cơ sở (lớp 7 đến lớp 9) là dạng toán cho một tam giác bất kỳ, một góc với 2 cạnh hoặc 3 cạnh. Việc của bài toán sẽ yêu cầu các bạn tìm ra được cạnh còn thiếu hoặc góc trong một tam giác. Có thể sẽ khó hơn hoặc nhiều bước trước đó, điều này đòi hỏi các kiến thức tổng hợp của các bạn trong các bài học trước.

Như vậy, các dạng toán với định lý Cosin cũng không quá đa dạng, nhưng nó sẽ đòi hỏi các bạn cần phải có kiến thức tổng hợp liên quan đến các bài học trước. Có như vậy mới nâng cao thành tích và dễ dàng tìm ra được đáp án đúng.

Lời kết 

Định lý cosin là một trong những công thức toán học kinh điển, được tạo ra bởi nhà toán học Al Kashi. Nắm vững các kiến thức về định lý Cos sẽ giúp các bạn rất nhiều trong việc học tập.