Cách áp dụng định lý Pytago vào làm bài tập

Định lý Pytago là một trong những kiến thức quan trọng nhất của nội dung hình học cơ bản mà bất kỳ học sinh nào cũng cần phải nắm chắc. Kiến thức Toán học này được phổ cập đến học sinh từ rất sớm, đây là kiến thức nền tảng, căn bản để học sinh tiếp tục học những kiến thức về hình học. Bài viết dưới đây sẽ cung cấp đến các em học sinh một số thông tin về định lý Pytago và Cách áp dụng định lý Pytago vào làm bài tập. 

1. Định lý Pytago là gì?

– Định lý Pytago hay còn gọi là định lý Pythagoras theo tiếng Anh. Định lý Pytago là một liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông.

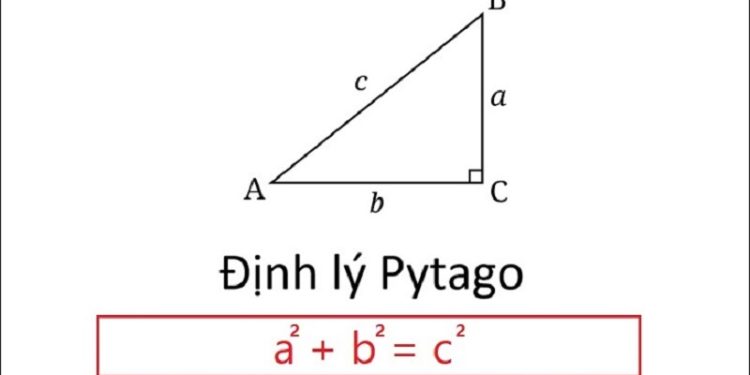
– Định lý Pytago phát biểu rằng trong 1 tam giác vuông bình phương cạnh huyền bằng tổng bình phương của hai cạnh góc vuông. Định lý có thể viết thành một phương trình liên hệ giữa độ dài các cạnh là a,b và c thường được gọi là công thức Pytago.

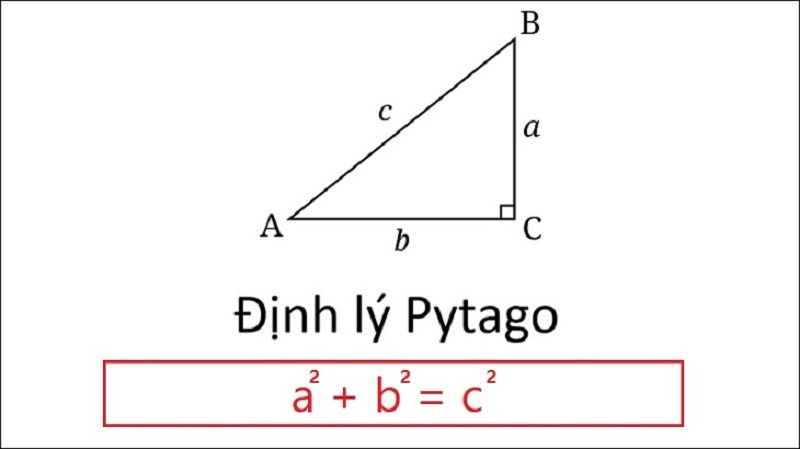
– Công thức Pytago: c² = a² + b²

– Trong đó, c là độ dài cạnh huyền; a,b là độ dài hai cạnh góc vuông

– Như vậy, trong bất kỳ 1 tam giác vuông nào thì bình phương cạnh huyền cũng sẽ bằng tổng bình phương hai cạnh góc vuông.

2. Định lý Pytago đảo

– Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh còn lại thì tam giác đó là tam giác vuông. Định lý Pytago đỏa được sử dụng rất phổ biến cũng như gồm nhiều ứng dụng trong thực tiễn, đây là một định lý toán học quan trọng hàng đầu của hình học cơ bản.

3. Những điều cần lưu ý khi học định lý Pytago

– Khi học định lý Pytago, để nắm chắc và áp dụng tốt trong quá trình làm và giải bài tập, học sinh cần lưu ý những điều sau:

+ Cạnh huyền của tam giác vuông luôn: Cắt ngang qua góc vuông mà không đi qua góc vuông. Đây là cạnh dài nhất của tam giác vuông, cạnh huyền được gọi là C trong định lý Pitago.

+ Khi tính, học sinh cần thường xuyên kiểm tra lại kết quả.

+ Khi nhìn vào hình, học sinh sẽ biết đâu là cạnh huyền vì đó là cạnh dài nhất đối diện với góc lớn nhất. Còn cạnh ngắn nhất sẽ đối diện góc nhỏ nhất của tam giác.

+ Ta chỉ tính được cạnh thứ 3 khi biết độ dài 2 cạnh còn lại trong tam giác vuông.

+ Nếu tam giác không phải là tam giác vuông, ta không thể áp dụng định lý Pytago mà sẽ tính được khi biết thông tin ngoài chiều dài 2 cạnh.

+ Học sinh nên vẽ tam giác để dễ dàng gán giá trị chính xác cho cạnh a,b và c. Đặc biệt, các bài toán từ và toán logic đều được áp dụng nhiều hơn cả.

+ Nếu chỉ biết số đo một cạnh, ta không thể dùng định lý Pytago để tính mà sẽ phải dùng hàm lượng giác.

4. Cách áp dụng định lý Pytago

4.1 Cách tìm cạnh của tam giác vuông

– Bước 1: Điều kiện tam giác đang xét phải là tam giác vuông

Định lý Pytago chỉ áp dụng được cho trường hợp tam giác vuông. Vì vậy, để tìm được các cạnh của tam giác vuông, hình tam giác đó phải có điều kiện là tam giác vuông với một góc bằng 90 độ. Học sinh có thể tìm thấy dấu hiệu hình tam giác vuông trên hình vẽ rất dễ dàng.

– Bước 2: Chỉ ra được các cạnh của hình tam giác vuông

Nhìn vào hình, người học cần chỉ ra 2 cạnh góc vuông và cạnh huyền. Cạnh luôn đối diện với góc vuông, là cạnh dài nhất sẽ là cạnh huyền. Hai cạnh ngắn hơn sẽ mặc định là 2 cạnh góc vuông.

– Bước 3: Xác định cạnh huyền cần tìm của tam giác vuông đó

Với định lý Pytago, ta có thể tìm được độ dài bắt kỳ của cạnh của một tam giác vuông nào bằng công thức trên chỉ cần biết chiều dài hai cạnh còn lại a² + b² = c². Có nghĩa là người học sẽ xác định cạnh chưa biết là a,b hay c. Nếu đã biết độ dài của 2 cạnh và 1 cạnh chưa biết của hình tam giác, người học sẽ có thể bắt đầu.

Ví dụ: Nếu người học đã biết cạnh huyền và một trong các cạnh bên còn lại sẽ dễ dàng tính được cạnh thứ 3 theo công thức ở trên.

Nếu có hai cạnh chưa biết độ dài, người học cần xác định một cạnh nữa mới có thể sử dụng định lý Pytago. Người học cần dùng hàm lượng giác cơ bản để tìm độ dài của một cạnh nữa nếu biết số đo của một góc nhọn trong tam giác đó.

– Bước 4: Thay giá trị độ dài hai cạnh vào phương trình a² + b² = c²

Trong đó, a, b là hai cạnh góc vuông; c là cạnh huyền

Ví dụ: a = 3, c= 5 ta có 3² + b² = 5²

– Bước 5: Tính bình phương

Giải phương trình, người học tính bình phương mỗi cạnh đã biêt. Nếu đơn giản, người học để ở dạng số mũ rồi tính sau.

Ví dụ: 9 + b² = 25

– Bước 6: Tách biến chưa biết sang một vế của phương trình

Nếu tính từng bước chi tiết, người học sử dụng phép toán tính số hạng của tổng để chuyển hai số đã biết sang một bên của phương trình và số chưa biết sang một bên của phương trình.

Ví dụ: b² = 16

– Bước 7: Giảm bình phương của cả hai vế phương trình

Kết quả b² = 16 cho thấy một vế của phương trình còn một biến bình phương còn vế kia là một số xác định. Giảm bình phương của cả hai vế ta sẽ có được b = 4. Như vậy kết quả của bài toán là 4, chiều dài số đa cạnh cần tìm là 4.

– Bước 8: Sử dụng định lý Pytago để tìm cạnh của tam giác vuông trong thực tế

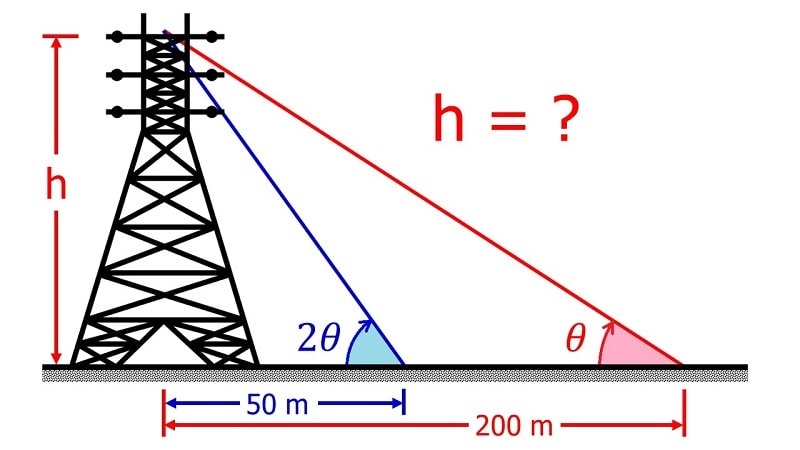
Định lý Pytago được sử dụng rất nhiều trong thực tế. Vì vậy, người học chỉ cần nhận biết tam giác vuông trong thực tế trong bất kỳ trường hợp nào. Áp dụng vào thực tế cuộc sống, chỉ cần 2 đường thẳng giao nhau hoặc 2 vật giao nhau tạo ra một góc vuông đồng thời có một đường thẳn hay vật thứ 3 cắt chéo qua góc vuông đã tạo ra một hình tam giác vuông. Từ đó, người học sử dụng định lý Pytago để tìm ra số đo 2 cạnh còn lại.

4.2 Cách tính khoảng cách giữa 2 điểm trong mặt X – Y 

– Bước 1: Xác đinh 2 điểm trong mặt phẳng X – Y

Dựa vào định lý Pytago, ta có thể dễ dàng tính được khoảng cách đường thẳng giữa 2 điểm trong mặt phẳn X – Y.  Lúc này, ta chỉ cần biết tọa độ x và y của 2 điểm bất kỳ. Bình thường tọa độ x, y sẽ được viết theo cặp thứ tự là tọa độ (x,y)

Muốn tìm khoảng cách giữa 2 điểm này, ta coi mỗi điểm là một trong những góc nhọn của tam giác vuông để thực hiện tính số đo chiều dài cạnh a, cạnh b sau đó tính tiếp độ dài cạnh c là khoảng cách giữa 2 điểm.

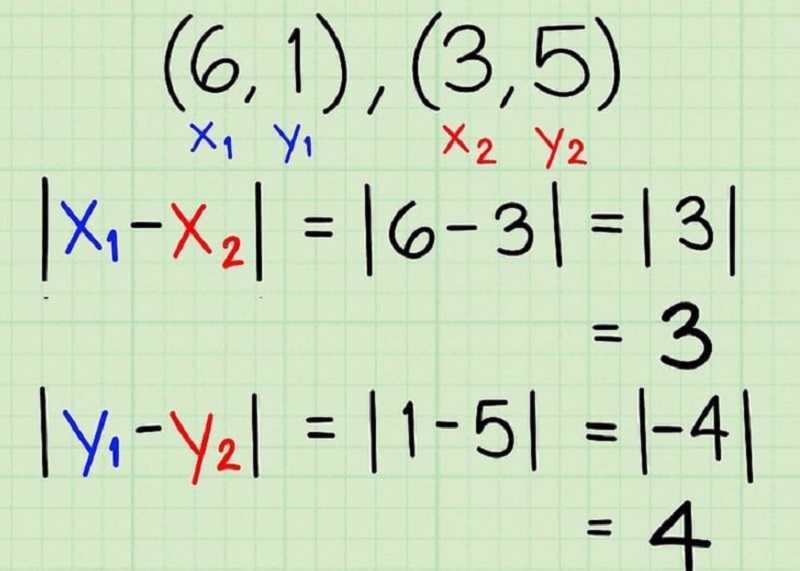
– Bước 2: Vẽ 2 điểm trên đồ thị

Tọa độ (x,y) trên mặt phẳng X – Y, trong đó x là tọa độ trên trục hoành, y là tọa độ trên trục tung. Từ đó, người học có thể tìm ra được khoảng cách giữa 2 điểm mà không cần vẽ đồ thị. Vẽ đồ thị ra, hình vẽ sẽ giúp ta nhìn trực quan và rõ ràng hơn rất nhiều.

– Bước 3: Tìm độ dài các cạnh góc vuông của tam giác

Dùng 2 điểm đã cho như các góc của tam giác ngay cạnh huyền, tìm độ dài cạnh góc vuông a và b. Người học có thể tính qua hình trên đồ thị hoặc dùng công thức tính Ix1 – x2I = I3 – 6I = I-3I = 3

Chiều dài cạnh thẳng đứng tính như sau: Iy1-y2I=I1-5I = I-4I = 4

Như vậy, hai canh còn lại của tam giác vuông này là a=3, b=4

• Bước 4: Dùng định lý Pytago giải phương trình tìm cạnh huyền

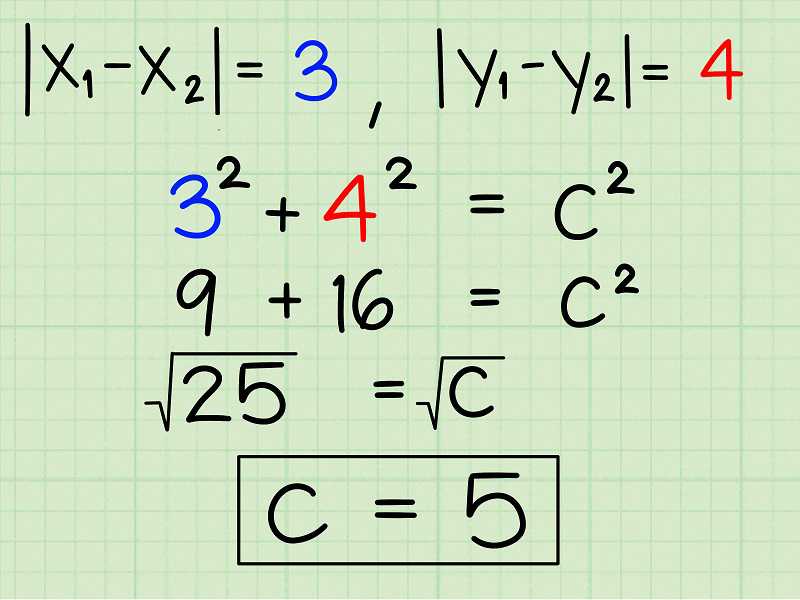
Trên đây là thông tin về định lý pitago và Cách áp dụng định lý Pytago vào giải bài tập. Hy vọng các em học sinh có thể áp dụng và làm bài tập một cách dễ dàng. Chúc các em học tốt!